In a
previous post
I looked at how the popular "Tandem-Match" Directional Coupler worked.
Recall from that analysis:
-
I analyzed the Tandem-Match coupler in terms of "lumped" circuit elements,
not distributed elements.
-
The coupler works by taking a sample of the voltage across the
transmission line at a single point and a sample of the current through
that point.
-
The Tandem-Match Coupler creates both of these samples with transformers.
-
The voltage at the "Forward Port" (that we measure on our meter) is
calculated by adding the current and voltage samples.
-
The voltage at the "Reflected Port" is calculated by
subtracting the current and voltage samples.
-
The voltage at the "Reflected Port" is 0 when the load is a real
resistance equal to the value of the resistors terminating the measurement
ports (Forward and Reflected Ports). Thus, the resistor values
should be selected to be the same as the characteristic impedance, Zo, of
the transmission-line system into which the the coupler is inserted.
-
I explained operation of the coupler both in terms of Forward and
Reflected waves and also without using waves, instead in terms of only the
voltage driving the coupler and the load at its output port.
Another popular directional coupler topology for HF is known as the Bruene
Coupler. This coupler was used in the
Collins 302C-3 Directional Wattmeter
and it was also described in an article written by Warren Bruene in
QST magazine ("An Inside Picture of Directional Wattmeters,"
QST, Apr., 1959).
I'll analyze the original design as well as some of the variants it
inspired. Again, I will use lumped-element analysis, and I'll present
explanations in terms of forward and reflected waves and also in terms of the
voltage being applied to the coupler and the load connected to its output
port.
My goal is to present you with an explanation that is understandable -- this
will
not be a rigorous analysis. So, when possible, I will take
advantage of models and assumptions that will simplify the math and hopefully
help you grasp the underlying principles.
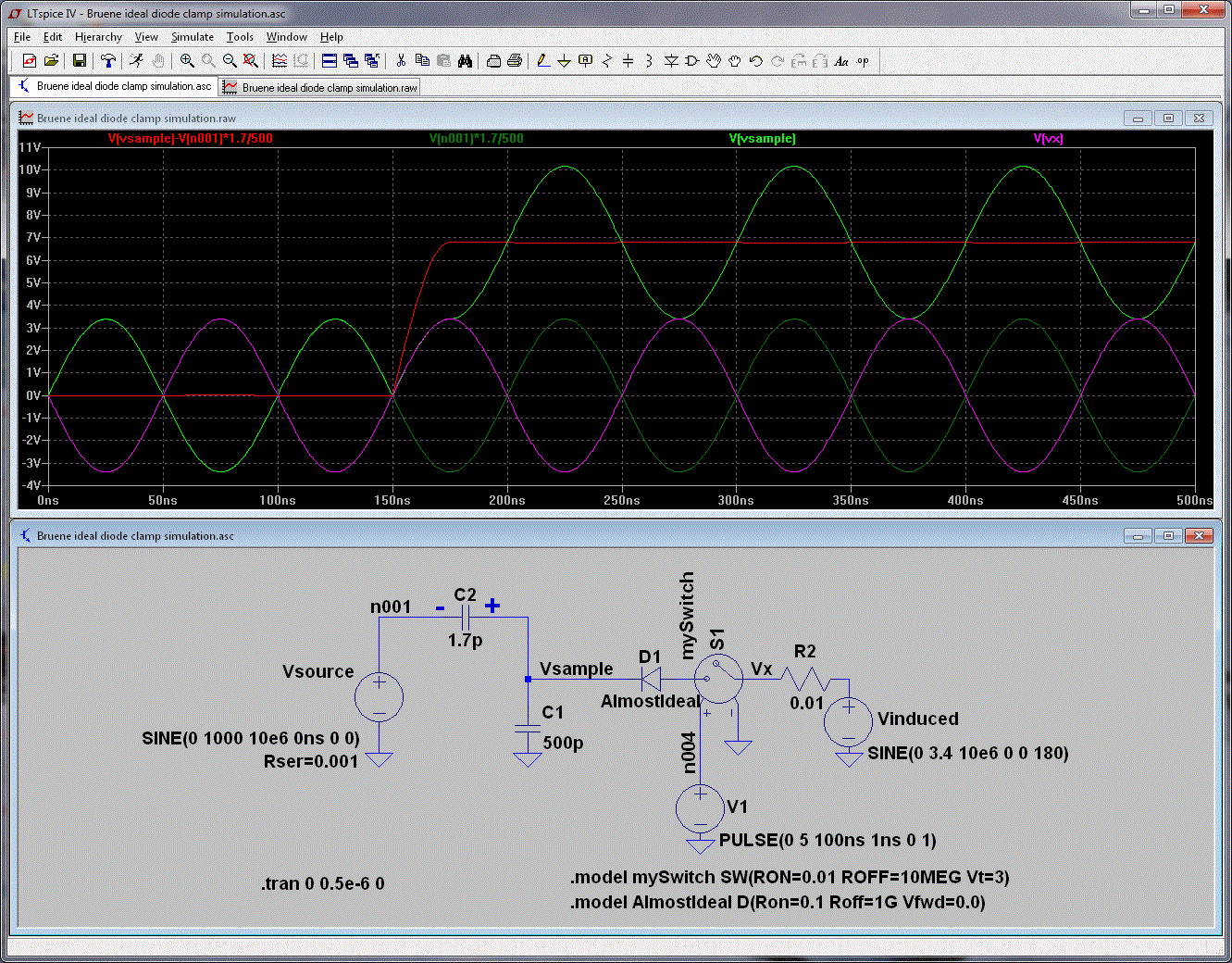
So here we go! Let's start with the schematic of the Bruene Coupler:
(click on image to enlarge)
There are two capacitive voltage dividers; one is used for generating the Vref
voltage, the other is used for the Vfwd voltage. Let's call these the
voltage samples, but in fact, they are more than that because of the two
diodes connected to them.
Line current passing through the 1-turn primary of a 1:60 turn transformer and
induces current in the 60-turn secondary. This current, in turn, is
transformed into voltage as it passes through the two 10 ohm
resistors. One voltage is positive with respect to ground, the
other is negative. These two voltages represent the current sample.
Now the explanation gets a bit tricky. Take a look at the schematic --
we're measuring Vref and Vfwd
at the voltage-divider taps.
This means that the two caps comprising each voltage-divider aren't simply
generating a voltage divided down from the line voltage, they are also
involved in adding or subtracting the current-sample voltages, too, so that,
when we measure the voltage across either 500 pf cap, it's actually the sum or
difference of voltage and current samples.
It wasn't obvious to me how the summing/differencing of voltage and current
samples at the voltage-divider nodes was being accomplished. It turns
out the diodes linking the voltage-dividers and the current samples play a
crucial role -- they are creating a DC voltage at the voltage-divider "tap" to
which their Cathodes are connected. But not as series rectifiers -- the
diodes instead are serving as "shunt" rectifiers.
The DC voltage they create is a function of the phase and amplitude
differences between the voltage and current samples. I'll explain the
role these caps and diodes play in more detail as it's interesting, but it's
also a a bit complex. So instead let me kick off this post with an
analysis of a Bruene variant that isn't quite so daunting.
(I'll get back to Bruene's original circuit, but it will be in another blog
post -- look for
Part 2!).
And before I get any further into this discussion, let me also make this
important point:
I will first look at the Bruene Coupler in terms of Forward and Reflected
waves. The Bruene Coupler, being made of "lumped elements" (in the first
example below: 2 capacitors, 1 transformer, and 1 resistor), is only looking
at the voltage and current present at its output port. It has no idea
what the load is, or even how the load is connected to the port. The
load might be a resistor or other component simply clipped onto the output
connector with test leads, or it might be a length of transmission line with a
load (either known or unknown) at its other end.
Irrespective of what the load actually is (transmission line, clipped-on
component, or whatever), the Bruene Coupler gives us voltage readings that can
be interpreted in terms of Forward and Reflected waves. It is important
to remember:
these readings should only be interpreted as representing actual
Forward and Reflected waves when the Bruene Coupler is connected in a
transmission line with the same
characteristic impedance, Zo, as the Coupler's designed-for target
impedance!
I'll start this analysis assuming the Bruene Coupler is inserted into a
transmission line of the
designed-for (target) characteristic impedance, Zo. I will follow
that with a look at its operation in a non-transmission line environment.
Bruene Coupler Variant, ZL1AN
ZL1AN has written an excellent
article
explaining a variation on Bruene's original coupler design, and I strongly
recommend you take a look at it. Tthe Heathkit HM-102 (and I believe
also the Drake W4) used this version of the circuit. I'll simplify the
analysis a bit by assuming that the current-sampling is done with an ideal
transformer.
Here's ZL1AN's circuit:
(click on image to enlarge)
Let's take this circuit and add a bit more information...
(click on image to enlarge)
In the image above:
-
"V" is the voltage across the transmission line at our "point" of
measurement. We will assume that the voltages are the same at the
input and output ports of the coupler -- there is no drop through the
coupler.
-
"I" is the current on the transmission line through that point.
-
I've replaced the resistor load (of resistance "R" ohms) across the
transformer secondary with two series resistors of value R/2.
-
The voltage at the junction of these two resistors is Vc, because the
voltage at the center-tap of the transformer is Vc, and these two resistor
form a divide-by-2 voltage divider across the secondary that essentially
places their junction at the same voltage as the center-tap.
-
Current "I" through the transformer primary induces a current "Is" in the
secondary.
-
Is = I/(2*N), and it flows in the opposite direction of I (per the
transformer "dots" that I've shown).
-
We assume that no current flows out either the Vfwd or Vref measurement
ports.
-
Therefore there is no load on our capacitive divider's voltage "Vc" (that
is, there isn't another path from Vc to ground that parallels the path
through C2).
- Therefore the voltage at Vc is:
Vc = V*(1/(jw*C2)) / ((1/(jw*C1))+(1/(jw*C2)))
If 1/(jw*C1) >> 1/(jw*C2), this simplifies to: Vc = V*C1/C2
(click on image to enlarge)
Vfwd and Vref are easily calculate from the series addition of Vc and the
appropriate voltage generated by the current sample:
Vfwd = Vc + Is*R/2
Vref = Vc - Is*R/2
Substituting in our equations for V and Is, we get:
Vfwd = V*(C1/C2) + I*R/(4*N) (equation 1)
Vref = V*(C1/C2) - I*R/(4*N) (equation 2)
Analysis Using Forward and Reflected Waves
Let's first analyze this circuit in terms of Forward and Reflected waves
passing through our coupler.
The Forward and Reflected waves each have a voltage and a current: Vf and If
are the voltage and current of the forward wave, and Vr and Ir are the voltage
and current of the reflected (or reverse) wave.
(click on image to enlarge)
The total voltage on the line, V, at any point is the sum of Vf and Vr at that
point.
V = Vf + Vr
And the total current on the line, I, at any point is the
difference of
If and Ir at that point (they subtract because Ir is flowing in the opposite
direction of If).
I = If - Ir
We also know:
If = Vf/Zo
Ir = Vr/Zo
Where Zo is the characteristic impedance of the transmission line.
So, substituting and rearranging, equations 1 and 2 become:
Vfwd = (Vf+Vr)*(C1/C2) + (Vf/Zo - Vr/Zo)*R/(4*N)
Vref = (Vf+Vr)*(C1/C2) - (Vf/Zo - Vr/Zo)*R/(4*N)
Regrouping terms:
Vfwd = Vf*((C1/C2) + R/(4*N*Zo)) + Vr*((C1/C2) - R/(4*N*Zo))
Vref = Vf*((C1/C2) - R/(4*N*Zo)) + Vr*((C1/C2) + R/(4*N*Zo))
Notice what happens if we select our components such that they meet the
following requirement:
C1/C2 = R/(4*N*Zo) = K (equation 3)
The two equations reduce down to:
Vfwd = Vf*2*K
Vref = Vr*2*K
So, if we select C1, C2, R, and N such that the satisfy the relationship
above, then the voltage we measure at Vfwd is solely related Vf, the voltage
of the Forward wave, and the voltage we measure at Vref is solely related to
Vr, the voltage of the Reflected (or Reverse) wave!
Analysis in a non-Transmission Line Environment:
It's instructional to analyze the operation of the directional coupler just in
terms of the components themselves, the voltage applied to the coupler, and
the load at its output port without using the concepts of waves. After
all, the coupler consists of lumped-elements, so there's no real reason to
think of its operation in terms of waves.
So let's draw our circuit like this, where V is the voltage source driving the
input of the Bruene Coupler and Zload is connected to its output.
We'll use the same assumptions that we used above. Therefore equations 1
and 2 still hold:
Vfwd = V*(C1/C2) + I*R/(4*N) (equation 1)
Vref = V*(C1/C2) - I*R/(4*N) (equation 2)
This time, rather than expressing V and I in terms of waves, we will note that
"I" is simply "V" divided by Zload:
I = V/Zload
If we substitute this equation into equations 1 and 2, we get:
Vfwd = V*((C1/C2) + R/(4*N*Zload)) (equation 4)
Vref = V*((C1/C2) - R/(4*N*Zload)) (equation
5)
Now let's take equation 3:
C1/C2 = R/(4*N*Zo) = K (equation 3)
Let's take that second half:
R/(4*N*Zo) = K
And rearrange it:
R/(4*N) = K*Zo (equation 6)
Where Zo can be considered to be our "Target" impedance. Usually this is
selected to be the impedance of the transmission line, but it needn't be.
Now let's plug equations 3 and 6 into 4 and 5 and reduce. We get:
Vfwd = V*K*(Zload + Zo)/Zload
Vref = V*K*(Zload - Zo)/Zload
Well, these are interesting equations. If Zload equals our target Zo
that we selected our components for (e.g. 50 ohms), then Vfwd = V*2*K and Vref
= 0.
We could use these equations as they are, but note what happens if we take
these two voltages and divide one into the other. We get something that
ought to look familiar:
Vref/Vfwd = (Zload - Zo) / (Zload + Zo)
Which is the definition of Reflection Coefficient!
So we can use the voltages measured at Vref and Vfwd to determine an impedance
relationship (i.e. imbalance) between the actual Zload and coupler's "target"
impedance of Zo. And this impedance relationship is exactly the same as
the Reflection Coefficient.
SWR is easily calculated from the Reflection Coefficient:
SWR = (1 + |Reflection Coefficient|) / (1 - |Reflection Coefficient|)
Note that, although SWR implies the presence of Forward and Reflected waves,
we have no guarantee that what we measure (or calculate) to be SWR or
Forward/Reflected power is actually what is happening in our system.
I'll quote
G3YNH:
"[The bridge] can only infer the existence of reflected power from the
difference between the actual load impedance and the target load
impedance. To understand this point, consider an SWR bridge designed to
balance when the load is 50+j0Ω. If we connect this bridge directly
to a 100Ω load resistor, it will declare an SWR of 2:1. The resistor is
not reactive however, and so will absorb all of the power delivered to it
and reflect none. The 2:1 SWR reading is only true when the bridge sees an
impedance magnitude of 100Ω (or 25Ω) at the input to a 50Ω transmission
line. The bridge is just an impedance bridge, it has no special psychic
powers, and its readings are only true when it is inserted into a line
having the same characteristic resistance."
So, summing up:
It should be evident from the above analysis that we don't need to rely on the
concepts and Forward and Reflected waves to understand how the Bruene coupler
operates.
Our typical "Bruene" SWR meter is really just calculating a relationship
between the load at its output port (Zload) and its own design parameters
(i.e. C1/C2 = R/(4*N*Zo) = K
). And this relationship is
equivalent to the Reflection Coefficient if "Zo" in the relationship: "C1/C2 =
R/(4*N*Zo) = K" is the same as the characteristic impedance of the
transmission line, should the coupler be connected to a transmission line.
It's important to note that Zload could be a load connected directly to
the coupler's "OUT" port with a couple of wires, or it could be the impedance
"presented" to the port by a long length of transmission line (an impedance
determined, at that point, by the interaction of the Forward and Reflected
waves).
The coupler doesn't care "how" the load is connected to its OUT port.
It's just looking at the voltage across the OUT port and the current through
the OUT port. It doesn't know anything else about the load except for
this voltage and current relationship
at its OUT port. For
example, if the OUT port happens to be connected to a transmission line, the
coupler has no knowledge of the line's Zo. It doesn't even know if there's a
transmission line attached, nor that the impedance it sees at its OUT port
might be due to the interaction of Forward and Reflected waves.
For this reason,
never assume that the meter reading is the
actual Reflection Coefficient, Γ, or that the SWR reading is the actual
SWR reading of the line. It might not be. We are really just
measuring the relationship between Zload (as it appears at the OUT port) and
the design parameters of the coupler.
Only if the "Zo" in the design relationship "C1/C2 = R/(4*N*Zo) = K" equals the
actual characteristic impedance, Zo, of the transmission line would
we truly be measuring the Reflection Coefficient.
And on that note, I'll end this non-Transmission Line analysis!
Frequency Insensitivity:
If you refer back to the equations for Vfwd and Vref, you should notice
something interesting: there are no j*w terms (where omega (w) =
2*pi*frequency). This means that the voltage-divider voltage, Vc, and
the voltage generated by the current-sample via the transformer are both
constant over frequency.
Of course, in the real world nothing is perfect and there will be effects due
to strays and parasitics. Never the less, if designed correctly (to deal
with strays), the frequency response should be flat over a broad range of
frequencies.
Which leads to an interesting observation: If the voltage divider is
independent of frequency, why use capacitors?
Well, one doesn't need to use caps, we could just as easily use inductors
(whose "jw" terms will cancel), or even resistors!
Which leads me to another variant of the Bruene coupler, which can be found in
G3SEK's "In Practice" column in the September, 2002 issue of
Radcom...
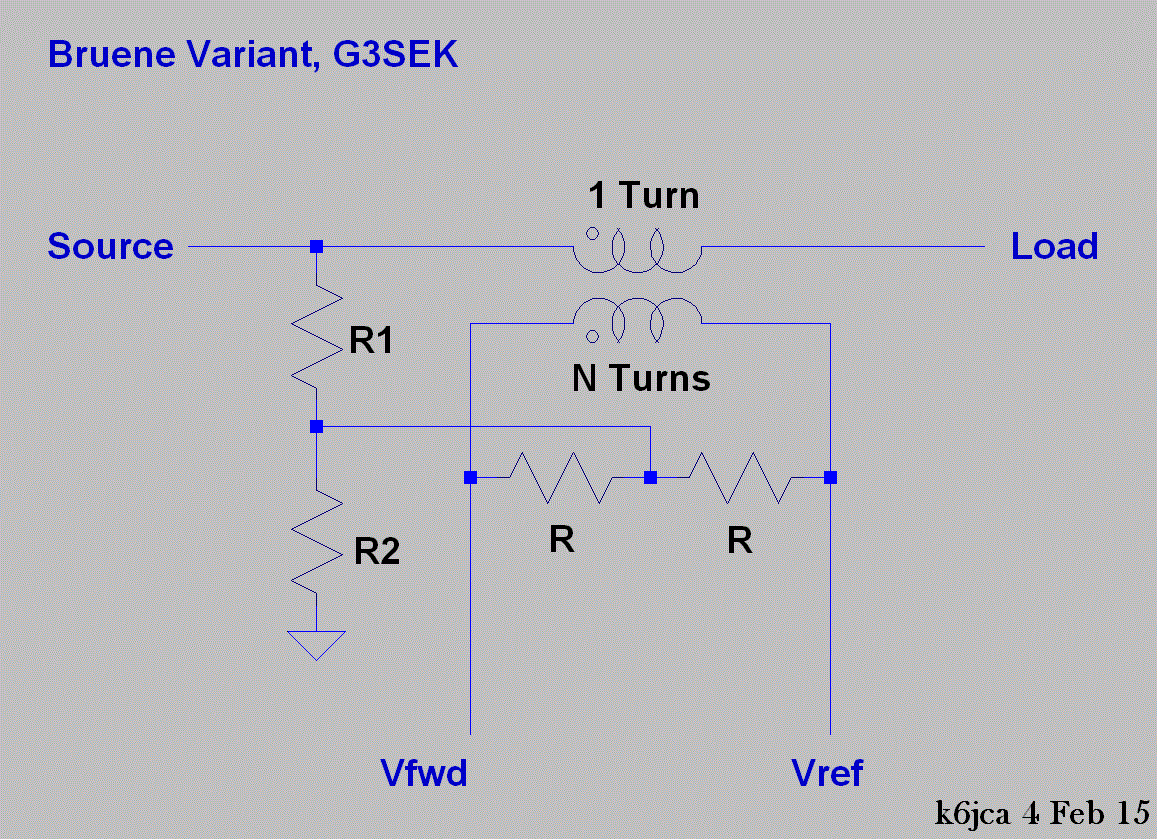
Bruene Coupler Variants, G3SEK:
One of the coupler's described in G3SEK's column looks very similar to the
coupler described by ZL1AN, but there are a few differences:
The first is that a resistive voltage divider replaces the capacitive voltage
divider.
The second is that the voltage sample from the resistor divider now feeds the
junction of two resistors instead of the transformer center-tap.
I'll skip analysis -- the process is no different that what we've done earlier
in this post.
Frankly, I don't know if it's better to feed the voltage-sample to the
common-point between two resistors, as done above, or to the center-tap of the
transformer secondary, as done by ZL1AN. Our concerns are: what is
the effect on Directivity, and what is the effect on Frequency Response?
Other Riffs on the Same Theme:
Vc can feed both the resistors and the transformer center-tap. (Any
negative effects? I don't know.)
The common point between the two resistors could be tied to ground. But
I'm not sure I'd recommend this -- it puts the two resistors in parallel with
C2, which means that the frequency response of Vc will no longer be
flat. (The secondary of the transformer acts as an
auto transformer, and thus, if Vc feeds its center-tap, it will look like a low impedance
(i.e. short) to its two ends. Which is to say -- it doesn't act as a
common-mode choke when feeding the center-).
Here's another interesting variation, found on
G3YNH's website
(worth a visit!). A single core is used, but the secondary consists of
two windings that are
not interconnected. Thus, two voltage
dividers are necessary in order to create voltage samples for the two
independent windings.
Analysis is similar to the other variants. Voltage and current samples
add on the left-hand side. And they subtract on the right-hand
side. I don't know what the advantage is to doing it this way,
though. But one advantage might be that the transformer's secondary, no
longer center-tapped, doesn't act like a "shorting" auto-transformer to Vc's
common-mode path to ground. Now, there is some impedance in the path
(due to the inductance of each of the secondary coils), but I'm not sure how
effective this would be, as it will depend upon the resistance "R" of the two
resistors which parallel these coils.
That covers the variants that I've seen that are obviously similar to the
ZL1AN topology (and thus will analyze in a similar fashion). I'll
introduce below a few more variants that stray a bit further afield (but not
by much).
The models presented thus far are in some cases simplified models of the
actual circuits. I've left off components that might be related to
frequency compensation, or detection, or other functions deemed secondary,
because I felt they would detract from understanding the underlying theory of
operation. If you're interested in more details, please click on the
links I've provided!
As to the positives and negatives for each topology, I wish I had some
answers, but I don't. If you have any experience or thoughts on the subject,
please feel free to let me know, either via comments to the post or email.
Continuing on...
Bruene Variant, W7EL:
Here's an interesting take on the Bruene Coupler, published by
W7EL in the Feb, 1990 issue of QST magazine.
Per the article, this version has +/- 7% accuracy over the range of 1 to 432
MHz. Quite impressive!
At first glance the design looks similar to the Tandem-Match coupler, but it
really is a variant on the Bruene topology; the current sample is either
added-to, or subtracted-from, the voltage sample. (With the Tandem-Match
coupler, it's the voltage sample that is either added-to, or subtracted-from,
the current sample).
The two transformers to ground create two voltage samples of the same polarity
and whose value is V/N, where V is the voltage on the line.
The "series" transformer samples the line current, I, and its secondary
generates a current that is I/N in amplitude.
If "I" is flowing from left-to-right in the diagram below (into the 1-turn
primary's "dot"), the secondary current runs from left-to-right (out of the
secondary's "dot"). This current creates a positive voltage of amplitude
I*51/N across the left-hand resistor and a negative voltage (w.r.t. ground)
across the right-hand resistor of amplitude -(I*51/N).
The voltage samples generated by the two voltage-sampling transformers are in
series with their respective resistors, and thus Vfwd is the sum of the
positive voltage across the left-hand resistor and the positive voltage across
left-hand secondary, while Vref is the sum of the
negative voltage
across the right-hand resistor plus the positive voltage across the right-hand
secondary.
The only negative that I can see with respect to the design is that you need
to wind 3 transformers!
Bruene Variant, N2PK Power Meter:
N2PK cleverly used the differential inputs of the AD8307 Log Amplifier to do
the summing and differencing of the voltage and current samples in his
homebrew
Power Meter.
That's it for the analysis of Bruene variants! Analysis of the actual
Bruene design will follow in Part 2...
Links to my Directional Coupler blog posts:
Notes on the Bruene Coupler, Part 2
Notes on the Bruene Coupler, Part 1
Notes on HF Directional Couplers (Tandem Match)